An inequality is a statement that two quantities are not equal. Inequalities may contain a variable.
Some examples of inequalities:
- x > 3
- 2y ≤ 8
- x + 5 > 4
- y – 12 ≥ 4
Graphing the Inequality Solution
After you get a solution, you’ll be asked to graph the solution. We will graph the solutions on a number line.
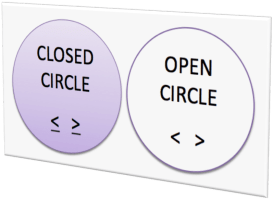
- If the inequality is < or >, you’ll use an open circle to mark the number portion of the inequality.
- If it is ≤ or ≥ then you’ll use a closed circle.
Values of the variable that make the inequality true are solutions to the inequality. A number line can be used to show the solutions to an inequality. The number line below shows the inequality x < 4.

Writing Inequalities
We will also be solving word problems with inequality equations. When converting words to inequalities there are some commonly used phrases that you need to memorize and become familiar with.
See the chart below:
| Phrase | Symbol Used | Example | Inequality |
|---|---|---|---|
| Fewer than | < | Fewer than ten students studied for the exam. Let s equal the number of students that studied. | s < 10 |
| No more than | < | The cost of c was no more than twenty | c < 20 |
| At most | < | The time t to take an exam should take at most fifty minutes. | t < 50 |
| Not less than | > | In order to pass an exam, she must make not less than a 70. | g > 70 |
| At least | > | To get an “A”, the percent p must be at least a ninety. | p > 90 |
Steps to Writing an Inequality
- Write down the variable.
- Write down the inequality symbol based on the key words used in the sentence.
- Write down the number in the sentence.
I will show you several examples. Work carefully. If you’re still struggling with solving equations, you’ll need to go back and review. This section will be difficult if you haven’t figured out how to solve one-variable equations.
(source)